贝利相位(或几何相位)，是一个系统在闭合的参数空间轨迹上，绝热地演化一圈后所累积的额外相位。类似于Aharonov-Bohm相位，贝利相位对量子系统的许多物理性质会产生重要影响，并带来一系列新奇的物理效应，例如石墨烯中的半整数量子霍尔电导，晶体中布洛赫电子的电极化、轨道磁矩效应，绝热输运中的量子电荷泵浦等等。除此之外，贝利相位也和材料的拓扑性质紧密联系在一起：如果一个体系中电子的贝利相位非零，那么该体系的布里渊区中往往具有非零的贝利曲率分布，体系也会因此表现出一些拓扑非平庸的性质，如反常霍尔效应、自旋霍尔效应等等。通常来说，一个材料体系的贝利相位是一个常数，且在实验上不容易被改变。直到最近，随着对贝利相位的深入研究以及实验技术的进步，人们发现可以在实验上调控贝利相位的大小。例如在单层石墨烯谐振腔中，利用外加磁场人们可以调节贝利相位等于0或\pi两个量子化值[1,2]。把贝利相位的调控和谷电子学相结合，通过调控贝利相位来调控材料的谷自由度是当今凝聚态物理中一个重要的前沿研究课题[3]。

与单层石墨烯相比，双层石墨烯的贝利相位可以从0连续地变化到2\pi，同时双层石墨烯中的准粒子也具有谷自由度，因此该体系为研究贝利相位与谷电子学的关系提供了一个完美的平台。最近，何林教授课题组利用低温强磁场超高真空扫描隧道显微镜（STM）系统在双层石墨烯量子点中实现了对贝利相位的连续调控，并通过贝利相位调控了该体系的谷极化。基于最新发展的edge-free量子点方法[4,5]，何林教授组在STM针尖下方的双层石墨烯中产生量子点，在单电子精度上测量量子点中受限态的简并度和对称性破缺，并系统测量了其在磁场下的演化（图1）。通过与理论合作者的深入合作和分析，他们判断实验上观察到的现象来源于受限态中不同谷能级在磁场下发生劈裂和交叉：量子点内K'谷的第零能级(k,0)和K谷的第零能级(K',0)在磁场下发生了劈裂，并在某一磁场下和K谷的第一能级(K,1)发生交叉(见图1(d))。基于半径典的 EBK量子化理论可以很好地定量解释实验现象。由于量子点的受限作用，电子的作用量积分中会同时出现轨道磁矩和贝利相位项。电子在两个谷中所获得的贝利相位会诱使谷能级发生劈裂。当磁场为零的时候，两个谷中电子在动量空间的绕行轨迹受到时间反演对称性的保护完全相同，因此电子的贝利相位也相同；增大磁场，K谷的电子绕行轨迹受到等效洛伦兹力的拉伸会增大，从而导致贝利相位也增大，而K’谷的电子绕行轨迹则在相反的等效洛伦兹力作用下被挤压，因此贝利相位则会减小(图2)。除此之外，两个谷中相反的轨道磁矩在磁场下也会诱导一个谷能级的劈裂。两个谷中贝利相位在磁场下的相反行为，使得他们的差值越来越大，从而和轨道磁矩一起，导致量子点内两个谷的受限能级出现巨大的劈裂；进一步的劈裂则又会导致不同谷中相邻能级的交叉行为。

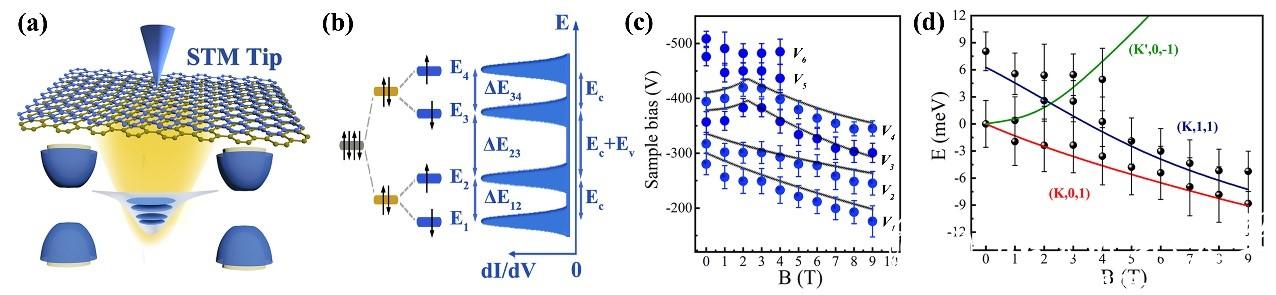
图1. (a),(b) 针尖电势产生双层石墨烯量子点及单电子峰示意图。(c) 受限态偏压随磁场的变化。(d) (k',0,1),(K',0.-1) 以及 ()K',1,1)谷能级随磁场的变化。

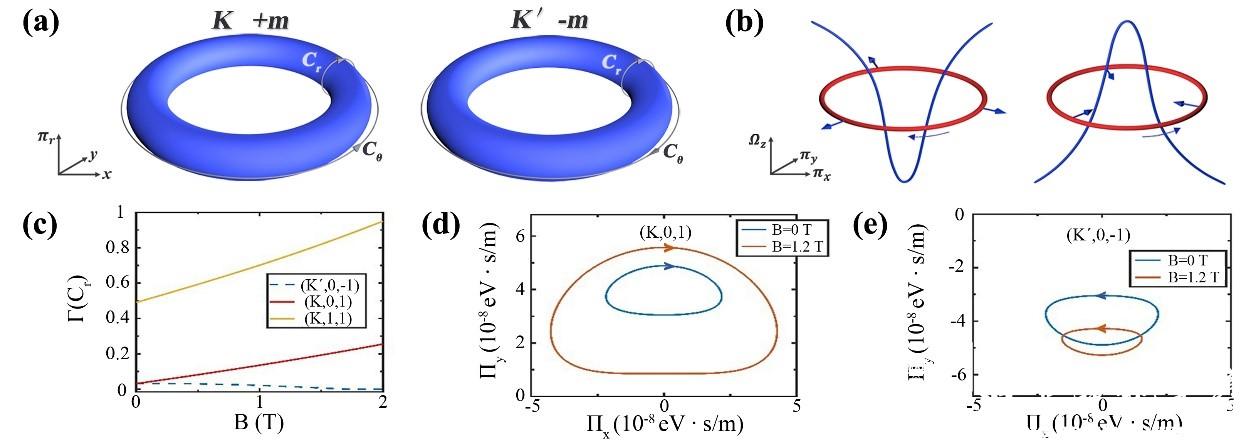
图2. (a) K谷+m角动量以及K'谷-m角动量的闭合回路.(b)(K,n,m)\(K',n,-m)两个谷的动量轨迹(红色环路)以及贝利曲率(蓝色曲线)。增加磁场，动量轨迹方向相反。(c) 不同谷贝利相位随磁场的变化。(d),(e) 磁场为0 T 和1.2 T时，(K',0,1)和(K',0,-1) 的动量轨迹。

这一工作深入揭示了石墨烯体系中贝利相位和谷自由度的重要关系。实验中观察到的谷能级劈裂和交叉行为，也为人们利用贝利相位来操控谷自由度、设计新型的谷开关器件提供了新的思路，对谷电子学的发展具有深远的意义。相关成果近日以“Movable Valley Switch Driven by Berry Phase in Bilayer Graphene Resonators”为题刊发在物理学顶级期刊《Physical Review Letters》上[6]。何林教授课题组博士生刘亦文为第一作者，孙庆丰教授课题组的博士生侯哲和何林教授课题组的博士生李思宇为共同第一作者，北京大学孙庆丰教授和北京师范大学何林教授为本文通讯作者。

URL: https://link.aps.org/doi/10.1103/PhysRevLett.124.166801

DOI: 10.1103/PhysRevLett.124.166801

1.   F. Ghahari et. al., “ An on/off Berry phase switch in circular graphene resonators”, Science 356, 845-849 (2017).

2.   Z.-Q. Fu, Y. Zhang, J.-B. Qiao, D.-L. Ma, H. Liu, Z.-H. Guo, Y.-C. Wei, J.-Y. Hu, Q. Xiao, X.-R. Mao, L. He, "Spatial confinement, magnetic localization, and their interactions on massless Dirac fermions". Phys. Rev. B 98, 241401(R) (2018).

3.   Z. Hou, Y.-F. Zhou, X. C. Xie, and Q.-F. Sun, "Berry phase induced valley level crossing in bilayer graphene quantum dots". Phys. Rev. B 99, 125422 (2019).

4.   S.-Y. Li, Y. Su, Y.-N. Ren, and L. He, "Valley Polarization and Inversion in Strained Graphene via Pseudo-Landau Levels, Valley Splitting of Real Landau Levels, and Confined States". Phys. Rev. Lett. 124, 106802 (2020).

5.   S.-Y. Li, Y.-N. Ren, Y.-W. Liu, M.-X. Chen, H. Jiang, and L. He, "Nanoscale detection of valley-dependent spin splitting around atomic defects of graphene". 2D Materials 6,031005 (2019). 

6.   Y.-W. Liu, Z. Hou, S.-Y. Li, Q.-F. Sun, and L. He, “Movable Valley Switch Driven by Berry Phase in Bilayer-Graphene Resonators”. Phys. Rev. Lett. 124, 166801 (2020).