层间转角在层状堆垛的二维材料体系中提供了一个全新的自由度来调控其结构与性质。近几年，相关方面的研究引起了广泛的关注。早在2012年，何林课题组就开始关注转角对双层石墨烯结构和电学性质的影响，测量了不同转角双层石墨烯的两个范霍夫峰的峰间距能量与转角大小的关系[1]，并预言该体系中的准粒子具有可调控的手征性[2]，研究了应变结构在该体系产生的赝磁场和赝朗道能级[3]。2015年，何林团队发现双层转角石墨烯体系费米速度随角度减小而迅速下降，证明在转角为1.1度(第一魔转角)附近时费米速度降为零[4]，并于2017年，在转角接近魔转角的双层石墨烯体系观察到强电子-电子相互作用[5]。2018年初MIT的Pablo课题组在魔角双层石墨烯观察到电子-电子相互作用导致的关联绝缘体态和超导态，魔角双层石墨烯物性研究迅速成为过去两年凝聚态物理研究的最大热点。

近期，何林课题组发展了一套方法，能够可控地制备利于扫描隧道显微镜系统（STM）研究的双层转角石墨烯，并利用STM研究了小角度双层石墨烯的性质，深入探索该体系由于电子-电子相互作用导致的平带简并度解除和新奇强关联量子物态的关联。例如，何林课题组与合作者发现当小转角体系的平带被部分填充时，电子-电子相互作用会解除平带的谷赝自旋简并度，在体系中产生很大的轨道磁矩（每个莫尔约10μ_B），由于轨道磁矩和磁场的耦合，谷极化态的劈裂能量会随着外加磁场线性增大[6]。同样的结果也在应变引起的平带中观察到了，当双层石墨烯的转角接近魔角时，体系中微小的应变结构可以使两个范霍夫峰之间出现一个新的零能量平带（赝朗道能级），何林课题组与合作者发现电子-电子相互作用会解除赝朗道能级的谷赝自旋简并度，产生轨道磁性态[7]。这些结果表明小转角石墨烯体系是研究二维轨道磁性态和量子反常霍尔效应的理想平台。在角度大于魔角的小转角双层石墨烯中，何林课题组与合作者证明电子-电子相互作用依然会起重要作用，并有可能产生完全不同于魔角双层石墨烯的新奇强关联量子物态。例如在1.49度的样品中，他们证明电子-电子相互作用解除了体系平带中的自旋和谷赝自旋的简并度，产生了一种全新的自旋和谷极化的金属态[8]，这一结果进一步拓宽了转角体系新奇强关联量子物态的研究范围。

除了电学性质受层间转角的调制，在双层转角石墨烯体系，由于层间堆垛能与层内晶格畸变引起的应变能的竞争，其原子结构也会随着角度发生改变。最近，何林课题组系统研究了双层转角石墨烯结构随着角度的演化，发现当转角大于魔角时，体系可以看作两个独立的刚性石墨烯层发生扭转，层内晶格畸变几乎可以忽略（定义为非重构结构）；当转角小于魔角时，由于莫尔条纹周期较大，层间堆垛能占主导，从而引起晶格畸变产生堆垛的畴界（domain wall）网格（定义为重构结构）。这种畴界的两边都是Bernal堆垛的双层石墨烯（分别为AB堆垛和BA堆垛），能传输谷极化的电流（图一）。我们利用STM证明非重构和重构的两种结构在魔角附近都能稳定存在。进一步，我们发现利用STM针尖脉冲可对魔角双层石墨烯的非重构和重构结构进行切换，从而开关其二维导电拓扑网格。同时，我们发现在强关联效应中起到重要作用的魔角双层石墨烯平带的带宽也能在这一过程中被调控[9]。相关成果近日刊发在物理学期刊《Physical Review Letters》上。何林教授课题组博士生刘亦文为第一作者，美国洛斯阿拉莫斯国家实验室的苏赢博士为文章的共同第一作者，何林教授为通讯作者。

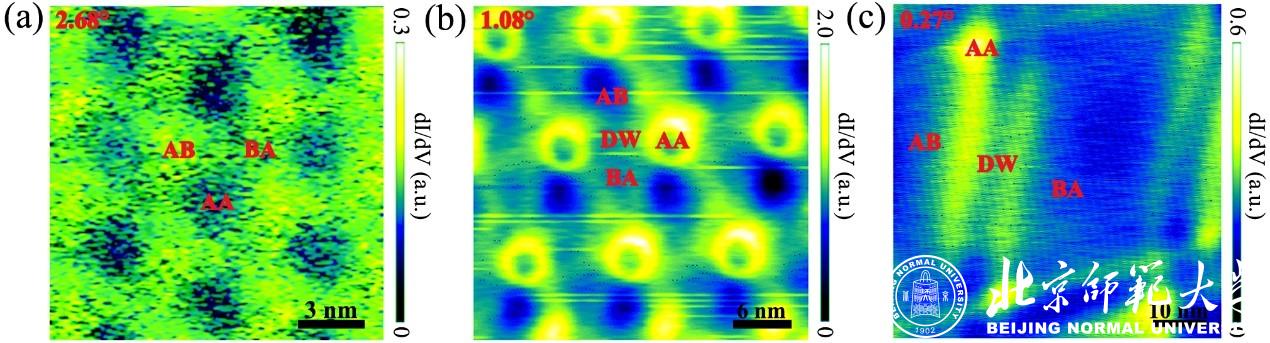
图1 不同转角双层石墨烯的电子态实空间分布。在转角小于魔角的双层石墨烯中能观察到清晰的畴界形成的导电网格，这种畴界能传输拓扑保护的谷极化电流（c图）。

上述工作得到了国家自然科学基金委、科技部国家重点基础研究发展计划、中组部“万人计划”青年拔尖人才支持计划、教育部青年长江学者支持计划以及北京师范大学经费的支持。

论文详细信息：
[1] W. Yan, M. Liu, R.-F. Dou, L. Meng, L. Feng, Z.-D. Chu, Y. F. Zhang*, Z. F. Liu, J.-C. Nie, and L. He*, “Angle Dependent Van Hove Singularities in a Slightly Twisted Graphene Bilayer”. Phys. Rev. Lett. Vol: 109, PP. 126801, (2012).
[2] W. Y. He, Z.-D. Chu, and L. He*, “Chiral tunneling in a twisted graphene bilayer”. Phys. Rev. Lett. Vol: 111, PP. 066803, (2013).
[3] W. Yan, W. Y. He, Z.-D. Chu, M. Liu, R.-F. Dou, L. Meng, L. Feng, Y. F. Zhang, Z. F. Liu, J.-C. Nie, and L. He*, “Strain and curvature induced evolution of electronic band structures of Twisted Graphene Bilayer”. Nature Commun. Vol: 4, PP. 2159, (2013).
[4] L.-J. Yin, J. B. Qiao, W. J. Zuo, W. T. Li, and L. He*, “Experimental evidence for non-Abelian gauge potentials in twisted graphene bilayers”. Phys. Rev. B Vol: 92, PP. 081406(Rapid Communications), (2015).
[5] S.-Y. Li, K.-Q. Liu, X.-Q. Yang, J.-K. Yang, H. W. Liu, H. Jiang*, and L. He*, “Splitting of van Hove singularities in a slightly twisted bilayer graphene”. Phys. Rev. B Vol: 96, PP. 155416 (2017).
[6] S.Y. Li, Y. Zhang, Y.-N. Ren, J. Liu*, X. Dai, and L. He*, “Experimental evidence for orbital magnetic moments generated by moiré-scale current loops in twisted bilayer graphene” Phys. Rev. B Vol: 102, PP. 121406 (Rapid Communications) (2020). Selected as Editor’s Suggestion.
[7] Y. Zhang, Z. Hou, Y.-X. Zhao, Z.-H. Guo, Y.-W. Liu, S.-Y. Li, Y.-N. Ren, Q.-F. Sun*, and L. He*, “Correlation-induced valley splitting and orbital magnetism in strain-induced zero-energy flat band in twisted bilayer graphene near the magic angle” Phys. Rev. B Vol: 102, PP. 081403(Rapid Communications) (2020).
[8] Y.-N. Ren, C. Lu, Y. Zhang, S.Y. Li, Y.-W. Liu, C. Yan, Z.-H. Guo, C.-C. Liu*, F. Yang*, and L. He*, “Spectroscopic evidence for a spin and valley polarized metallic state in a non-magic-angle twisted bilayer graphene” ACS Nano Vol: 14, PP. 13081 (2020).
[9] Y.-W. Liu, Y. Su, X.-F. Zhou, L.-J. Yin, C. Yan, S.-Y. Li, W. Yan, S. Han, Z.-Q. Fu. Y. Zhang, Q. Yang, Y.-N. Ren, and L. He*, “Tunable lattice reconstruction, triangular network of chiral one-dimensional states and bandwidth of flat bands in magic-angle twisted bilayer graphene”. Phys. Rev. Lett. Vol: 125, PP. 236102 (2020).

本文转载自北京师范大学新闻网

原文链接：http://news.bnu.edu.cn/zx/xzdt/119839.htm